Gros

Nullcon 2019 - Singular

03 Jan 2019

tldr; discrete log on singular curve

Description:

Alice and Bob calculated a shared key on the elliptic curve
y^2 = x^3 + 330762886318172394930696774593722907073441522749x^2 + 6688528763308432271990130594743714957884433976x + 759214505060964991648440027744756938681220132782

p = 785482254973602570424508065997142892171538672071
G = (1, 68596750097555148647236998220450053605331891340)

(Alice's public key)
P = d1 * G = (453762742842106273626661098428675073042272925939, 680431771406393872682158079307720147623468587944)

(Bob's poblic key)
Q = d2 * G = (353016783569351064519522488538358652176885848450, 287096710721721383077746502546881354857243084036)

They have calculated K = d1 * d2 * G.
They have taken K's x coordinate in decimal and took sha256 of it and used it for AES ECB to encrypt the flag.

Here is the encrypted flag: 480fd106c9a637d22fddd814965742236eb314c1b8fb68e70a7c7445ff04476082f8b9026c49d27110ba41b95e9f51dc

We are given the curve over finite field, the base point G, two public keys (P and Q) and need to find corresponding prive keys.

As task’s name points, the curve is singular, meaning:

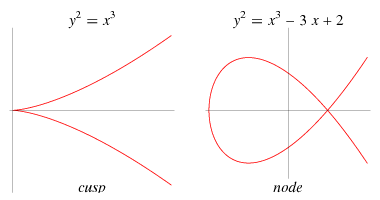Example singular curves Example singular curves, source: mathworld.wolfram.com

Now we need to find a map between points on the curve and elements of a field. Formal description (and proofs) are given in book “Elliptic Curves: Number Theory and Cryptography, 2nd edition” by Washington. In short the algorithm is:

We can find singular point with sage:

p = 785482254973602570424508065997142892171538672071
x,y = GF(p)['x,y'].gens()
P.<x,y> = GF(p)[]
f = x^3 + 330762886318172394930696774593722907073441522749*x^2 + 6688528763308432271990130594743714957884433976*x + 759214505060964991648440027744756938681220132782
C = Curve(-y^2 + f)
singular_point = C.singular_points()[0]
# (413400541209677581972773119133520959089878607131, 0)

As the points is not (0, 0) we translate curve (and all used the points):

f_ = f.subs(x=x+singular_point[0])

G = (1, 68596750097555148647236998220450053605331891340)
P = (453762742842106273626661098428675073042272925939, 680431771406393872682158079307720147623468587944)
Q = (353016783569351064519522488538358652176885848450, 287096710721721383077746502546881354857243084036)

G_t = (GF(p)(G[0]-singular_point[0]), GF(p)(G[1]))
P_t = (GF(p)(P[0]-singular_point[0]), GF(p)(P[1]))
Q_t = (GF(p)(Q[0]-singular_point[0]), GF(p)(Q[1]))

To determine if the curve is cusp or node we can count multiplicity of roots. Triple root means the curve is cusp and double that it’s node.

print f_.factor()
# x^3 -> cusp

For cusp the map is: \begin{equation} E(\mathbb{F}_p) \mapsto \mathbb{F}_p^{+}, \quad (x,y) \mapsto \frac{x}{y}, \quad \infty \mapsto 0 \end{equation}

Where $\mathbb{F}_p^{+}$ is additive group.

And in reverse: \begin{equation} t = \frac{x}{y}, \quad x = \frac{1}{t^2}, \quad y = \frac{1}{t^3} \end{equation}

To find d1 such that P = d1 * G (d2 such that Q = d2 * G) we simply need to divide x by y for every point and compute modular inverse:

G_m = G_t[0]/G_t[1]
P_m = P_t[0]/P_t[1]
Q_m = Q_t[0]/Q_t[1]

d1 = P_m * (G_m ^ (-1))
d2 = Q_m * (G_m ^ (-1))

Computation of K = d1 * d2 * G also can be done in the field. Then, to find x coordinate of the K, we use reverse map. At the end we need to translate the point back to our original curve:

K = d1 * d2 * G__
K_x = K^-2
K_x += singular_point[0]
print K_x
# 165140565353247266256196454126511228757085857653

Decrypted flag:

from Crypto.Cipher import AES
from hashlib import sha256
from binascii import *

K = sha256('165140565353247266256196454126511228757085857653').digest()
print(AES.new(K, AES.MODE_ECB).decrypt(flag_enc))
# hackim19{w0ah_math_i5_quite_fun_a57f8e21}

Note that there was similar challenge on hxp ctf 2018 with curve being node (task “curve12833227”).

Copyright © 2023